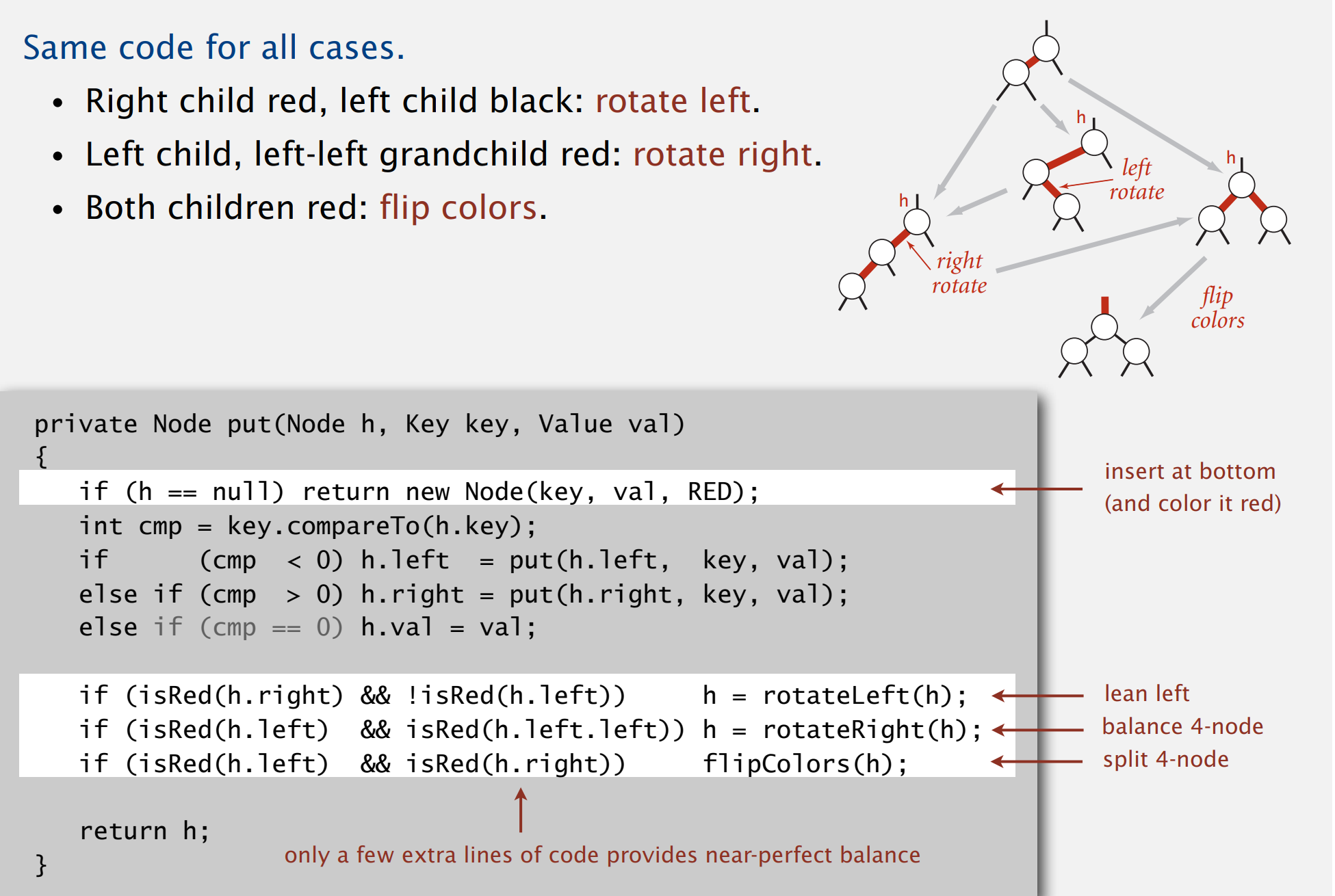
Doubly Linked List
什么是双向链表
双向链表是一种特殊的链表,其中的每个节点都包含前一个和后一个节点的引用。
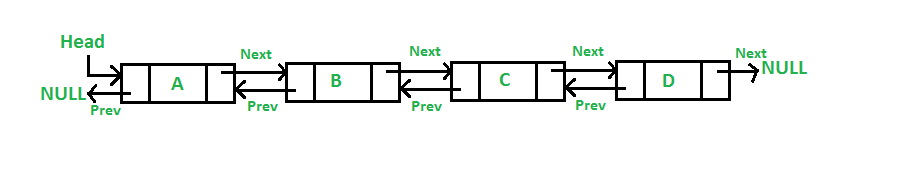
下面是一个双向链表的简单示例:
// Class for Doubly Linked List
public class DLL {
// Head of list
Node head;
// Doubly Linked list Node
class Node {
int data;
Node prev;
Node next;
// Constructor to create a new node
// next and prev is by default initialized as null
Node(int d) { data = d; }
}
}
# Node of a doubly linked list
class Node:
def __init__(self, next=None, prev=None, data=None):
# reference to next node in DLL
self.next = next
# reference to previous node in DLL
self.prev = prev
self.data = data
type Node struct {
Value int
Previous *Node
Next *Node
}
type LinkedList struct {
Head *Node
Length int
}
对比普通链表的优势
- 可以向前或者向后遍历
- 给定一个节点,如果需要删除它,双向链表比单向链表更快一些,因为你可以执行以下逻辑即可删除,而不需要再次查找一次节点的 prev
java
node.prev.next = node.next
node.next.prev = node.prev - 同理,给定一个节点,在其前面插入一个新的节点更快
对比普通链表的劣势
- 空间浪费:每个节点都要保存上一个节点的引用。使用 C++ 的一个示例可以解决空间浪费的问题,见此 https://www.geeksforgeeks.org/xor-linked-list-a-memory-efficient-doubly-linked-list-set-1/
- 因为多了一个引用,每次操作都需要更多的动作
应用场景
- 浏览器的前进和后退
- 很多程序的 undo 和 redo 功能
- LRU ( Least Recently Used ) / MRU ( Most Recently Used ) Cache
2-3 Search Tree
建议看 Coursera 上的视频 https://www.coursera.org/learn/algorithms-part1/lecture/wIUNW/2-3-search-trees,本章节的动画文件均由该视频截屏后转换。
- 概念和图
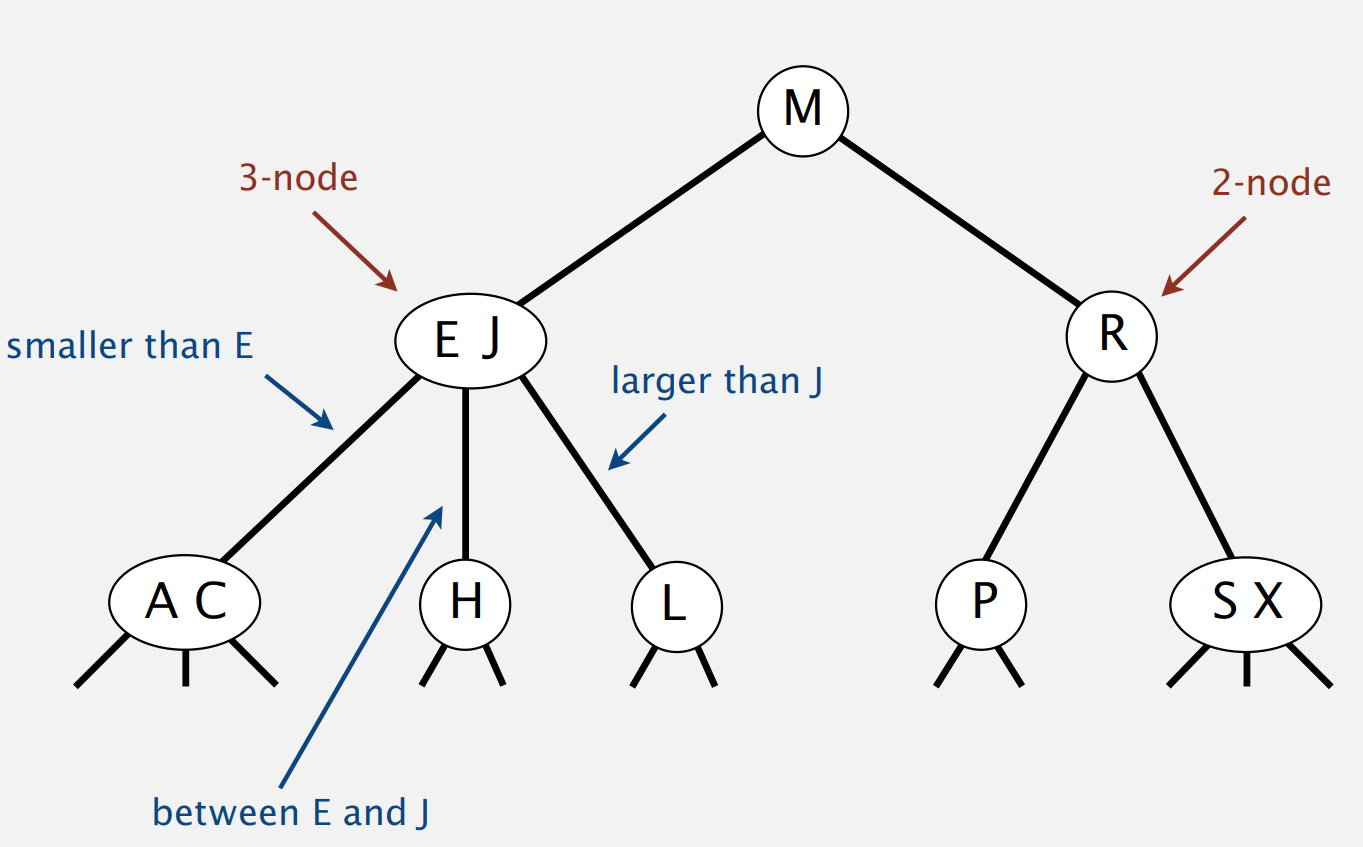
每个 node 允许 1-2 个元素- 2-node: 1 元素,2个子 node
- 3-node: 2 元素,3个子 node
- 从 root 到 null link 的每条路径都等长
- 2-3 tree demo 搜索的过程

- 2-3 tree demo 插入

插入到一个 3-node 会发生什么?

-
2-3 tree 构造过程

-
属性
始终维护对称和平衡。 -
性能
- 完美的平衡:每条从根节点到 null links 的路径都有相同的长度
- 树的高度:
- 最差情况:log2N,全部是 2-node
- 最好情况:log3N,全部是 3-node
- 12-20(100万node)
- 18-30(10亿node)
- 查询和插入操作对数级性能
Red Black BSTs
BST means binary search tree.
Left-leaning read-black BSTs
左倾红黑树:通过红色胶水(红线)将 3-node 中的两个元素粘起来
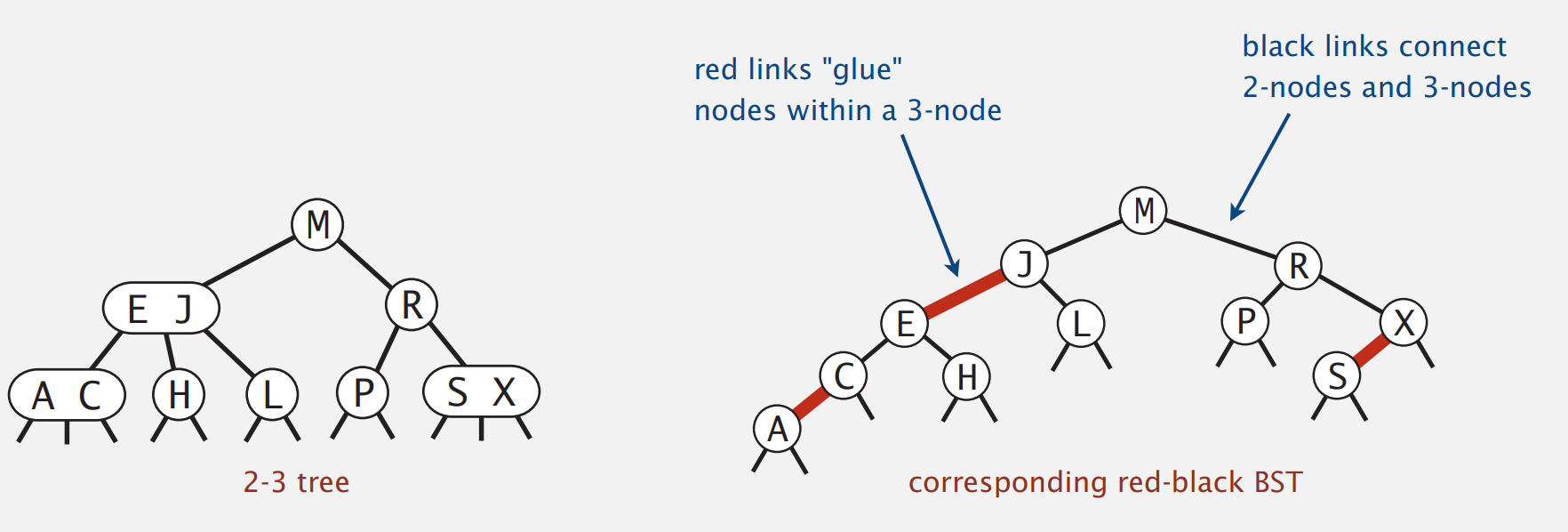
一个等价的定义
如果一个 BST 满足以下几个条件,那么它就是一个左倾红黑树(LLRB):
* 没有节点同时连接了两条红线
* 每条从 root 到 null link 的路径有相同数量的黑线(2-3树的特性)
* 红线向左倾斜
实际上,从任意一个节点到其子树的叶子节点经过的黑线都是相同的。
搜索忽略颜色,和普通的 BST 一致,但是因为其保持较好的平衡,通常更快。
public Val get(Key key){
Node x = root;
while (x != null){
int cmp = key.compareTo(x.key);
if (cmp < 0) x = x.left;
else if (cmp > 0) x = x.right;
else if (cmp == 0) return x.val;
}
return null;
}
因为每个节点和父节点相连的只有一条线,因此可以将颜色编码到代码里面
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node {
Key key;
Value val;
Node left, right;
boolean color; // 注意这里 color 是指连接父节点的线的颜色
}
private boolean isRed(Node x) {
if (x == null) return false; // null links are black
return x.color == RED;
}
上面的代码用图来解释,就是:
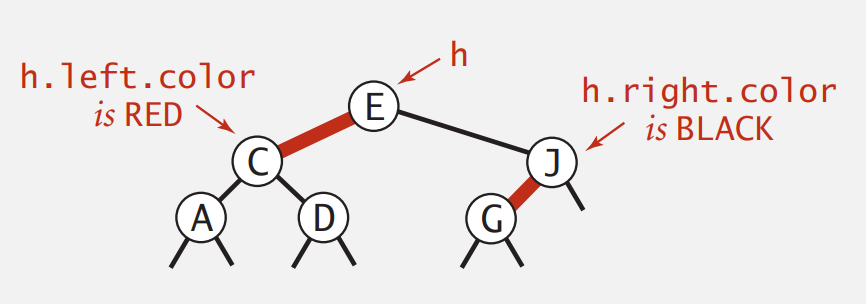
左旋(右旋同理,不变的是要维持树的平衡和对称)
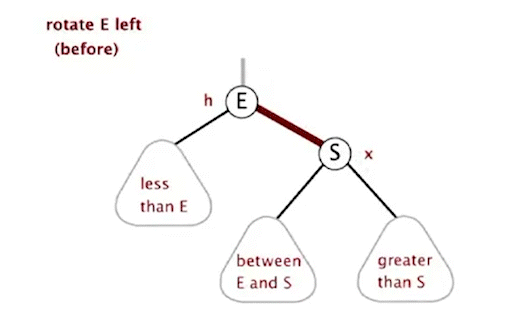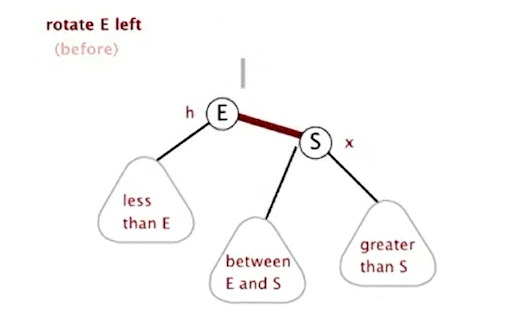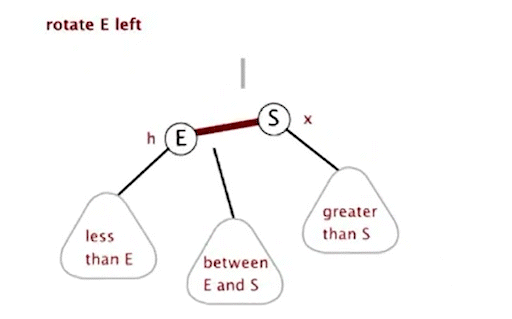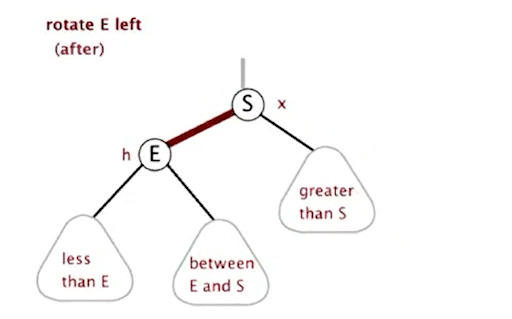
private Node rotateLeft(Node h) {
assert isRed(h.right);
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
return x;
}
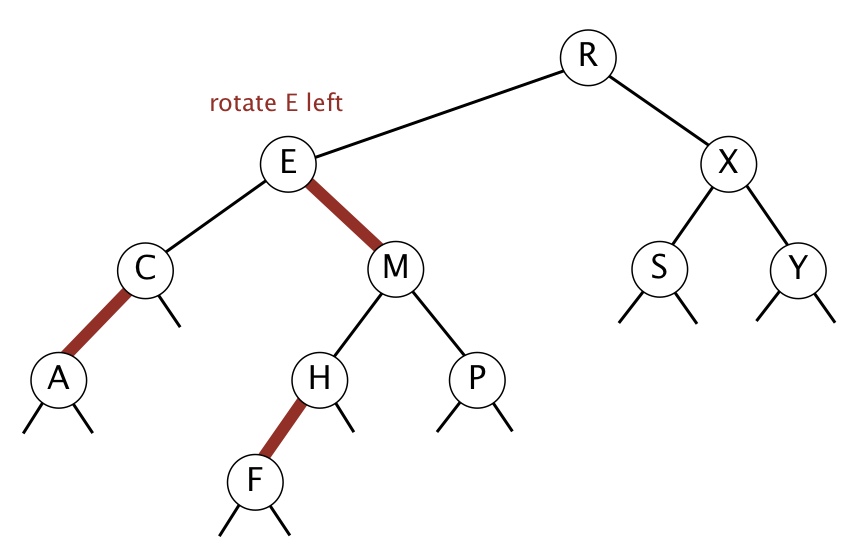
请回答,如果左旋以下 BST 中包含E的节点,那么左旋后的 BST 按照 level order 遍历是什么呢?(答案见评论。)
颜色反转(color flip)

插入:下图插入C,作为 2-3 tree 来考虑,插入到右侧,然后左旋

插入:直观展示
插入 255 个元素,按照最坏情况,从小到大插入
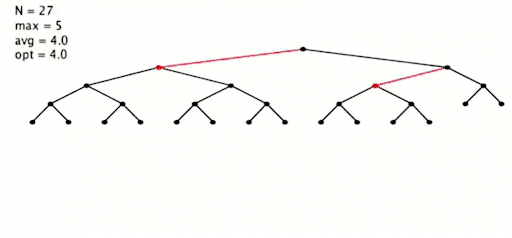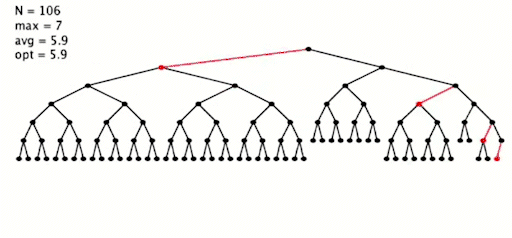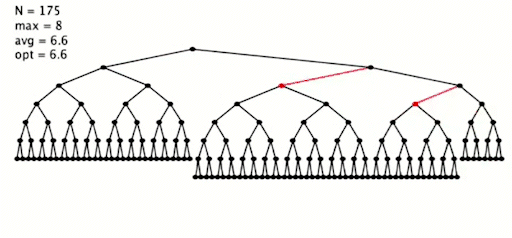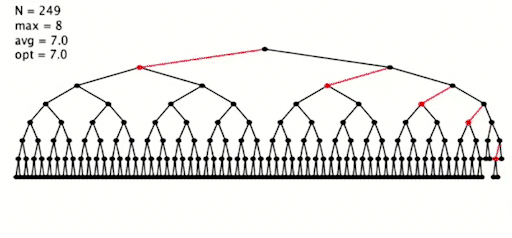
简单代码实现
- 左黑右红向左旋
- 左黑到底向右旋
- 两边都红颜色变