(Machine Translated)
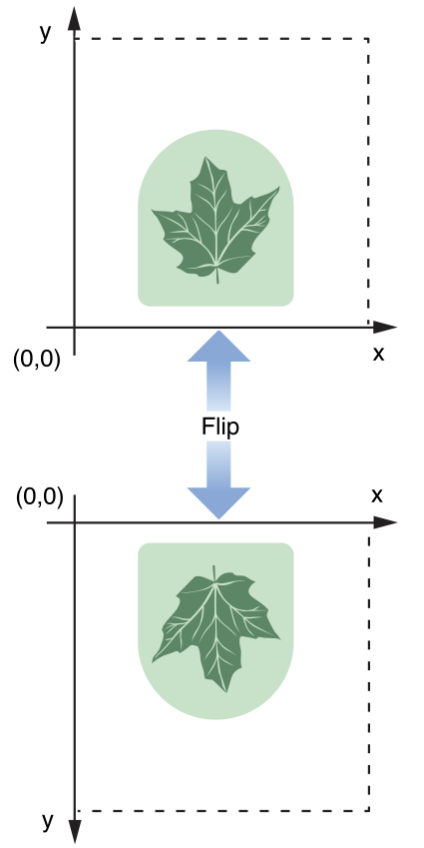
The coordinate system we use most is the standard Cartesian plane right-angle coordinate system, which takes the lower-left corner of the screen as the origin and increases the y coordinate upwards and the x coordinate to the right.
SCWindow’s coordinates, on the other hand, are flipped coordinates with the upper-left corner of the main screen as the origin, and the following is a simple comparison chart:
In real-world scenarios, especially with multiple screens, converting between two coordinate systems is still not an easy task.
Suppose there are two displays, arranged as shown below:
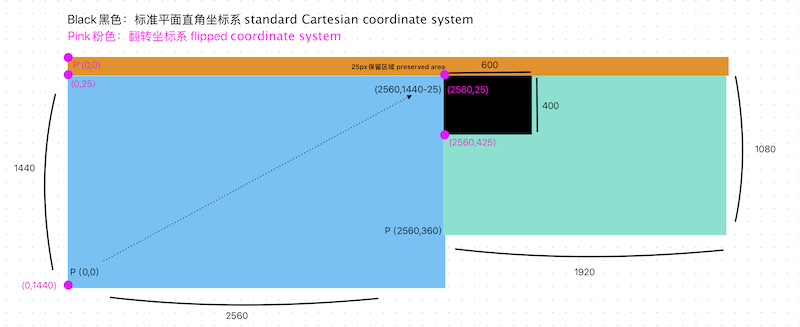
The black area is the target window, which is also the area of the SCWindow (if you use the SCContentSharingPicker, then this area is the SCContentFilter.contentRect returned by it), and we are going to compute the coordinates of the upper-left corner of the window in the planar right-angled coordinate system based on this area.
- main screen (2560×1440), lower-left corner origin (0,0), secondary screen (1920×1080), lower-left corner origin (2560,360).
- The primary and secondary screens will be aligned with each other, with the top edge aligned
- each screen will have a 25px reserved area that can be thought of as the status bar at the top of the system
As you can see, there are a lot of distractions. There’s the status bar, there are monitors of varying sizes and alignments that change all the time, and they don’t have the same origin.
All you have is the value of SCWindow.frame, you don’t realize at first that SCWindow.frame.origin is the flipped coordinate, and Apple doesn’t tell you this anywhere, such is the daily life of Apple software development.
The good thing is that after non-stop debugging, we were eventually able to figure out on our own that SCWindow was using the flipped coordinates.
So the answer to the above image is (2560,1440-25).
How about making some changes
Move the secondary screen down so that its bottom edge is aligned with the primary screen and the origin becomes (2560,0):
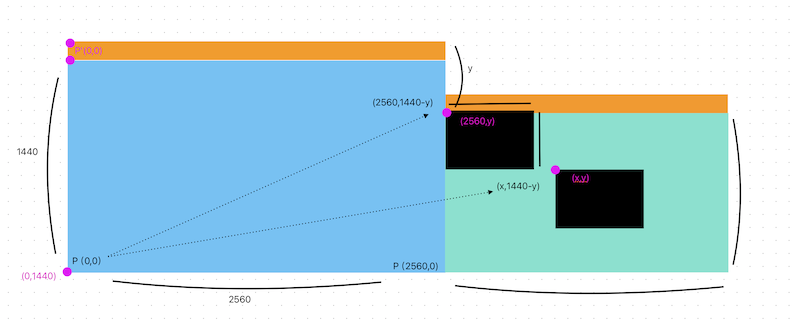
This time we know that the result we are asking for has nothing to do with the size of the secondary screen, so extraneous details are omitted.
The points of the planar Cartesian coordinate system where the upper left corner of the two black windows are located are shown in the figure.
As can be seen, the result is also independent of the size of the status bar.
So the result is (x-coordinate of the target window, height of the main screen – y-coordinate of the target window), which is (x, mainScreen.height-y)?
Move the secondary screen on top of the main screen to verify this.
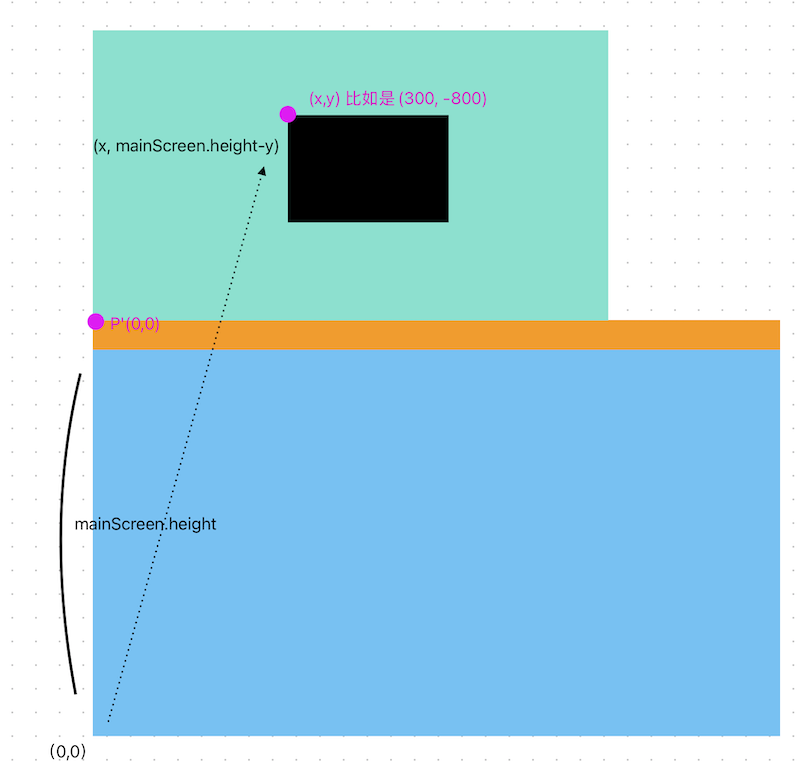
The points that appear above the flipped coordinate system have their y-coordinates become negative and smaller the higher up you go.
As you can see in the image, the point also displays correctly in the planar rectangular coordinate system according to our formula, (x, mainScreen.height-y).
This seems simple enough, but until you eliminate these confounding factors, this calculation is very error-prone.
This is part of the process of developing MagicToy’s always on top feature.
Always On Top in MagicToy
You can use ⌃ + left-click to top the window, or you can use the shortcut keys to select it. You can use the same ⌃ + left-click to untop an already-topped window, or, right-click to untop it in the pop-up menu.
You can also change these shortcuts to your favorite choices.
There are many other similar features in MagicToy, such as always-on-top, color picking, mapping, right-click menus, status bar management, ntfs, and many more features that will be added to the dozen or so later.
I am currently planning to put it on the App Store. How about this, is this a feature you want? Let me know.